SEGITIGA
Segitiga adalah bangun datar yang
mempunyai tiga sisi. Ketiga ujungnya
saling bertemu dan membentuk sudut. Jumlah sudut dalam segitiga adalah 180°.
B.
Unsur-
Unsur Segitiga
Unsur-unsur suatu segitiga terdiri
atas 3 ruas garis sebagai sisi segitiga dan 3 sudut yang masing-masing dibentuk
oleh sepasang-sepasang sisi-sisi segitiga tersebut.
Pada gambar diatas, sisi-sisi
segi-tiga dan sudut-sudut segitiga adalah:
AB = c. BC = a. AC = b
Ð A = α ; Ð B = β ; Ð C = γ
Untuk
membentuk suatu segitiga diperlukan 3 unsur, yang memenuhi persyaratan tertentu
(kecuali
ketiganya sudut). Beberapa alternatif pasangan ketiga unsur pembentuk segitiga
adalah :
(ss, ss, ss)
; (ss, ss, sd) ; (ss, sd, ss) ; (ss, sd, sd) dan (sd, ss, sd)
Dari
pasangan unusr yang diketahui untuk suatu segitiga, dapat ditentukan
unsur-unsur lain
yang tidak
diketahui.
Fungsi
trigonometri yang berlaku untuk sudut-sudut dalam segitiga memberikan beberapa
formula yang
menyatakan hubungan antara sisi-sisi dan sudut-sudut segitiga, sehingga
memudahkan
perhitungan unsur segitiga yang belum diketahui.
C.
Jenis –
jenis Segitiga
Jenis-jenis suatu segitiga
dapat ditinjau berdasarkan
a. panjang sisi-sisinya;
b. besar sudut-sudutnya;
c. panjang sisi dan besar
sudutnya.
1.
Jenis
Segitiga Ditinjau dari Panjang Sisi-sisinya
a.
Segitiga sama sisi
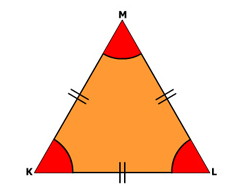
Segitiga sama sisi adalah segitiga yang mempunyai tiga sisi
sama panjang dan s emua sudutnya
sama besarnya yaitu 600.
Perhatikan gambar segitiga sama sisi
KLM di atas,
·
Panjang KL = LM = KM
·
Sudut K = Sudut M = Sudut L (
yaitu 600 )
b.
Segitiga sama kaki
Segitiga sama kaki adalah segitiga dengan dua sisinya yang sama panjang dan terbentuk dari dua segitiga siku-siku yang kongruen.
Segitiga sama kaki adalah segitiga dengan dua sisinya yang sama panjang dan terbentuk dari dua segitiga siku-siku yang kongruen.
Perhatikan
gambar segitiga sama kaki di atas,
·
Panjang PQ = PR ( PQ dan PR di sebut
kaki ).
·
Sudut Q = Sudut R ( di sebut
sudut-sudut kaki segitiga PQR ).
·
Sisi QR merupakan alas dan Sudut P
adalah sudut puncak.
c.
Segitiga sembarang
Segitiga sembarang adalah segitiga dengan ketiga sisinya tidak sama panjang dan juga sudut-sudutnya tidak sama besar.
Segitiga sembarang adalah segitiga dengan ketiga sisinya tidak sama panjang dan juga sudut-sudutnya tidak sama besar.
Perhatikan
segitiga sembarang ABC di atas ,
·
Panjang AB ≠ BC ≠ CA.
·
sudut A ≠ sudut B ≠ sudut
C.
2.
Jenis
segitiga ditinjau dari besar sudutnya.
Dilihat dari besar sudut-sudutnya
jenis segitiga di bedakan dalam tiga jenis yaitu :
a
Segitiga lancip
Segitiga yang memiliki tiga buah sudutnya berbentuk lancip dimana besar masing-masing sudutnya lebih dari 00 dan kurang dari 900 disebut dengan segtitiga lancip.
Segitiga yang memiliki tiga buah sudutnya berbentuk lancip dimana besar masing-masing sudutnya lebih dari 00 dan kurang dari 900 disebut dengan segtitiga lancip.
Perhatikan
gambar segitiga lancip ABC di atas,
·
Sudut A, sudut B dan Sudut C
merupakan sudut lancip.
b.
Segitiga siku-siku
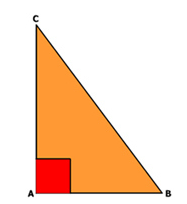
Segitiga dengan salah satu sudutnya berukuran 900 disenut dengan segitiga siku-siku.
Segitiga dengan salah satu sudutnya berukuran 900 disenut dengan segitiga siku-siku.
Perhatikan
gambar segitiga siku-siku ABC di atas,
·
Sudut A merupakan sudut siku-siku
yang ukurannya adalah 900.
c.
Segitiga tumpul
Segitiga yang salah satu sudutnya tumpul dimana salah satu sudutnya lebih dari 900 tetapi kurang dari 1800 di sebut dengan segitiga tumpul.
Segitiga yang salah satu sudutnya tumpul dimana salah satu sudutnya lebih dari 900 tetapi kurang dari 1800 di sebut dengan segitiga tumpul.
Perhatikan
gambar segitiga tumpul PQR di atas,
·
Sudut P merupakan sudut tumpul dari
segitiga tersebut.
3. Jenis-Jenis Segitiga
Dilihat Dari Panjang Sisi-Sisinya Dan Besar Sudut-Sudutnya
Dilihat dari panjang sisi-sisinya dan besar sudut-sudutnya segitiga di bedakan dalam tiga jenis yaitu :
a.
Segitiga
siku-siku sama kaki
Segitiga yang memiliki besar salah satu sudutnya 900 dan kedua sisinya sama panjang biasa di sebut dengan segitiga siku-siku sama kaki.
Segitiga yang memiliki besar salah satu sudutnya 900 dan kedua sisinya sama panjang biasa di sebut dengan segitiga siku-siku sama kaki.
b
Segitiga lancip sama kaki
Segitiga dengan sudut lancip dan kedua sisinya sama panjang di sebut dengan segitiga lancip sama kaki.
Segitiga dengan sudut lancip dan kedua sisinya sama panjang di sebut dengan segitiga lancip sama kaki.
c
Segitiga
tumpul sama kaki
Segitiga yang mempunyai salah satu sudutnya tumpul dan memiliki dua sisi yang sama panjangnya.
Segitiga yang mempunyai salah satu sudutnya tumpul dan memiliki dua sisi yang sama panjangnya.
D.
Sifat
– sifat segitiga
1. Jumlah
seluruh sudut di dalam bangun segitiga adalah 180°.
2. Teorema
Pythagoras
Untuk
segitiga siku- siku ABC berlaku Teorema Pythagoras, yaitu “ kuadrat sisi miring
sama dengan jumlah kuadrat sisi siku- sikunya.”
Teorema
Pythagoras
BC
² =AB² + AC² atau a² = b² + c²
3. Dua
segitiga kogruen
Perhatikan
gambar berikut ini !
Gambar
diatas merupakan gambar segitiga KLM yang kongruen dengan segitiga PQR. Dua
segitiga dikatakan kongruen (sama dan sebangun) jika dan hanya jika sisi-sisi
dan sudut –sudut yang bersesuaian sama besar yaitu:
a. Ketiga
sisinya sama panjang .
KL=PQ,
LM = QR, dan MK= RP
b. Sebuah
sisi dan kedua sudut apitnya sama besar.
LM
= QR,dan KL= PQ
d. Dua
sisi hipotenusa pada dua segitiga siku- siku sama panjang dan dua sisi lainnya
sama panjang pula. Segitiga KLM kogruen
dengan segitiga PQR , di notasikan dengan
4. Dua
segitiga sebagun
Perhatikan
gambar berikut !
Gambar
segitiga DEF sebagun dengan segitiga PQR. Dua segitiga di katakana sebagun (
similar) jika memenuhi syarat-syarat berikut.
a. Perbandingan
panjang sisi-sisi yang bersesuaian sama yaitu:
b. Sudut
–sudut yang bersesuaian sama besar, yaitu:
Segitia
DEF sebangun dengan segitiga PQR , dinotasikan dengan
E.
Luas
Dan Keliling Segitiga
K
= a+ b + c
L=
½ x alas x tinggi
atau
Dengan
s = ½ ( a + b + c )
CONTOH SOAL
1. Hitunglah keliling segitiga dengan
panjang sisi-sisinya 8 cm; 16 cm; dan 12 cm
.
Cara
penyelesaian :
Mencari keliling segitiga dapat
dilakukan dengan menjumlahkan seluruh sisi dari segitiga tersebut, maka
K
= a+ b + c
K= 8 cm+ 16 cm + 12 cm
K=36 cm
2. Hitunglah luas daerah masing-masing
segitiga pada gambar di bawah ini.
Cara
penyelesaian:
Luas
segitiga ABC dapat dicari dengan persamaan:
L.ΔABC = ½
x alas x tinggi
L.ΔABC = ½
x AB x BC
L.ΔABC = ½
x 8 cm x 6 cm
L.ΔABC =
24 cm2
3. Sebidang tanah berbentuk segitiga
dengan panjang tiap sisi tanah berturut-turut 4 m, 5 m, dan 7 m. Di sekeliling
tanah tersebut akan dipasang pagar dengan biaya Rp 85.000,00 per meter.
Berapakah biaya yang diperlukan untuk pemasangan pagar tersebut?
Cara penyelesaian:
Mencari keliling segitiga dapat
dilakukan dengan menjumlahkan seluruh sisi dari segitiga tersebut, maka
kllΔ = 4 m
+ 5 m + 7 m
kllΔ = 16
m
karena
biaya yang diperlukan Rp 85.000,00/m, maka
Biaya = 16
m x Rp 85.000,00/m
Biaya = Rp
1.360.000,00
Jadi biaya
yang diperlukan untuk pemasangan pagar tersebut adalah Rp 1.360.000,00
LATIHAN
SOAL
1. Sebuah taman berbentuk segitiga sama
kaki dengan panjang sisi yang sama 15 m, panjang sisi lainnya 12 m, dan tinggi
7 m. Jika taman tersebut akan ditanami rumput dengan biaya Rp. 60.000/m2,
hitunglah keseluruhan biaya yang diperlukan.
2. Diketahui segitiga ABC dengan garis
tinggi AD seperti gambar berikut.
Jika ∠BAC = 90°, AB = 4 cm, AC = 3 cm, dan
BC = 5 cm, tentukan
a. luas
segitiga ABC;
b. panjang
AD.
3. Diketahui luas sebuah segitiga
adalah 165 cm2 dan panjang alasnya 22 cm. Hitunglah tinggi segitiga.
KUNCI
JAWABAN
1.
Luas
bangun segitiga dapat dicari dengan persamaan:
L.Δ= ½ x
alas x tinggi
L.Δ = ½ x
12 m x 7 m
L.Δ = 42 m2
karena
biaya yang diperukan adalah Rp. 60.000/m2 maka biaya totalnya adalah
Biaya
total = L.Δ x biaya per meter persegi
Biaya
total = 42 m2 x Rp. 60.000/m2
Biaya
total = Rp.2.520.000,00
Jadi
keseluruhan biaya yang diperlukan adalah Rp.2.520.000,00
2.
a.
Karena ∠BAC = 90° salah satu kaki sudutnya
bisa dijadikan tinggi atau alas, maka
L.ΔABC = ½
x alas x tinggi
L.ΔABC = ½
x AB x AC
L.ΔABC = ½
x 4 cm x 3 cm
L.ΔABC = 6
cm2
b. panjang AD dapat dicari dengan
konsep luas segitiga yaitu
L.ΔABC = ½
x alas x tinggi
L.ΔABC = ½
x BC x AD
6 cm2
= ½ x 5 cm x AD
AD = 6 cm2/2,5
cm
AD = 2,4
cm
3.
L.Δ
= ½ x alas x tinggi
165 cm2 = ½ x 22 cm x
tinggi
165 cm2 = 11 cm x
tinggi
tinggi = 165 cm2/11 cm
tinggi = 15 cm
a.
Karena ∠BAC = 90° salah satu kaki sudutnya
bisa dijadikan tinggi atau alas, maka
L.ΔABC
= ½ x alas x tinggi
L.ΔABC
= ½ x AB x AC
L.ΔABC
= ½ x 4 cm x 3 cm
L.ΔABC
= 6 cm2
b.
panjang AD dapat dicari dengan konsep luas segitiga yaitu
L.ΔABC
= ½ x alas x tinggi
L.ΔABC
= ½ x BC x AD
6
cm2 = ½ x 5 cm x AD
AD
= 6 cm2/2,5 cm
AD
= 2,4 cm
